Wild concealed algebras are not g-tame
Aug 9, 2024· ·
0 min read
·
0 min read
Jacob Fjeld Grevstad
 Me giving talk
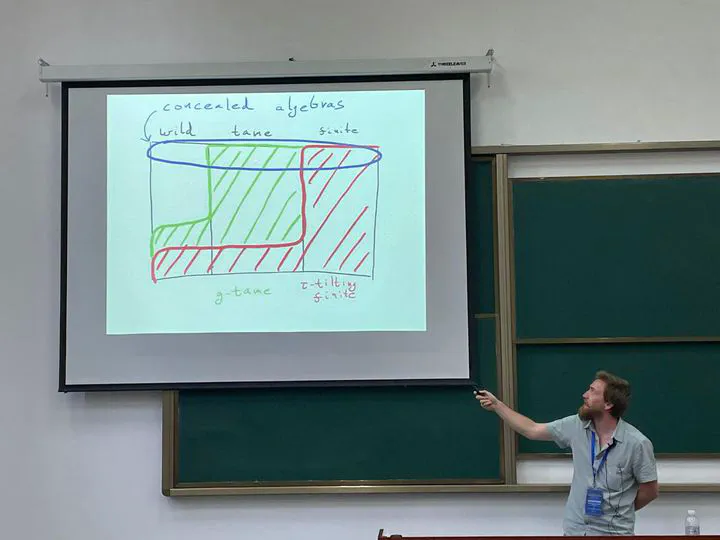
Me giving talkAbstract
The g-vector fan is a convex-geometric construction to study the τ-tilting theory of an algebra. Using it one extends the notions of tame representation type to τ-tilting theory, by saying that an algebra is g-tame if its g-vector fan is dense in ℝ^n. \ Tame algebras are always g-tame, but the converse is not true in general. \ In this talk we show that concealed algebras are g-tame if and only if they are tame. This also implies the same result for incidence algebras of simply connected posets. \ Joint work w/ Erlend Børve and Endre Rundsveen
Date
Aug 9, 2024 3:30 PM — 4:00 PM
Event
Location
SJTU Shanghai